
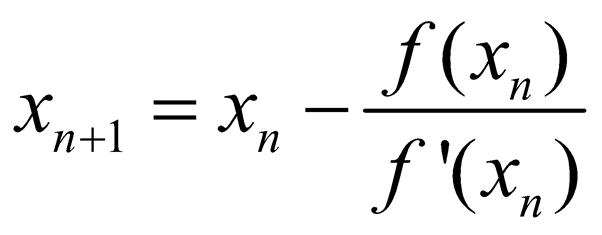
Newton raphson method blacksholes how to#
If you don’t want to read about the brute force method, skip ahead to the next section to learn how to implement the more efficient method – The Newton Rasphon Method.

Luckily, for our problem, there’s a more efficient solution. Usually, brute force is the last resort when everything else fails. This method will perform many calculations since we don’t know when there will be a match. When a calculated price is close enough to the observed price, the corresponding sigma is considered to be the “root”. The volatility (sigma) is unknown and we need to calculate it Calculating Implied Volatility In Python Brute Force MethodĪ “brute force” method basically attempts to use many different sigma (volatility) values to calculate the option price.Instead of calculating an option price, we already know it.The BS pricing formula sort of has what we need but does not exactly solve our problem. Return "Please specify call or put options." Below is the code: import scipy.statsĭ1 = (log(S/K) + (r+sigma**2/2)*t) / (sigma*sqrt(t)) In this tutorial, we implemented the BS formula in Python to calculate options prices. Black Scholes Option Pricing Formula In Python As its name suggests – it is implied and not explicitly known. All the input values are readily observable except for one – the implied volatility. The Black Scholes formula gives a framework to model the option prices and risks associated with an option. More seller than buyers, the price goes down.More buyers than sellers, the price goes up.In reality, option prices are determined by demand and supply. For practical reasons, we would prefer Newton’s method, and brute force is just for comparison. If we want to calculate the implied volatilities for all options, we have to use something fast. This tutorial covers two methods on how to calculate option implied volatility using Python: brute force and Newton Raphson Method.Ī single option chain contains thousands of values for different options.


 0 kommentar(er)
0 kommentar(er)
